Умножение одночлена на многочлен
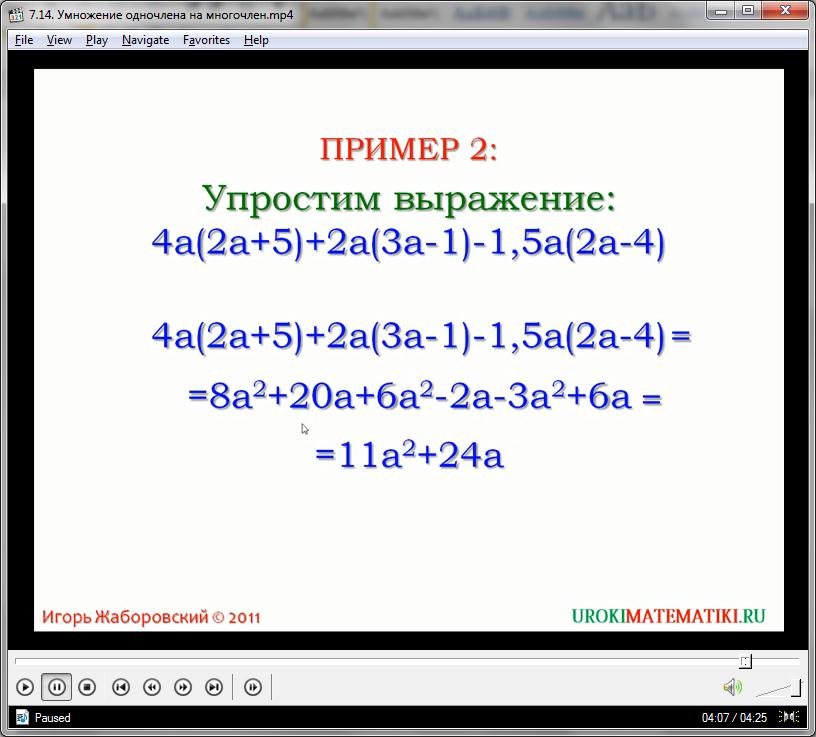
Мы знаем, как выполнять умножение одночлена на многочлен. Выясним, как умножать многочлен на многочлен. Таким образом, мы каждый член первого многочлена умножили на каждый член второго многочлена:.






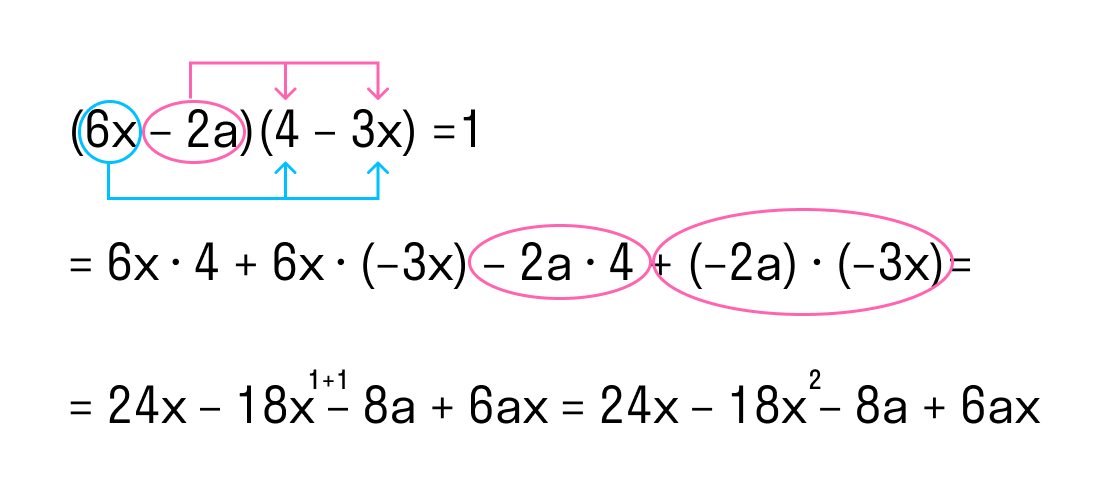


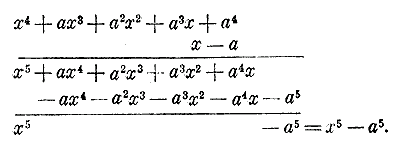
Если нет ни одного слагаемого, то такой многочлен называется нуль-многочленом, его степень точно не определена, но при этом считается меньшей любого неотрицательного числа. В более общем случае многочлен может содержать степени нескольких независимых переменных [ 3 ] x 1 , x 2 ,. Многочлены как функции можно складывать, перемножать, а в некоторых случая и делить один на другой [ 4 ].
- Содержание
- Проще говоря, многочлен это несколько одночленов, соединенных знаком «плюс». В некоторых многочленах одночлены могут соединяться знаком «минус».
- Поскольку мы уже умеем умножать многочлен на одночлен, обозначим второй многочлен буквой k и выполним умножение:.
- Автор: Беляева Ирина Владимировна Открытый урок по алгебре в 7 классе.










Одночленом мы назовем произведение чисел и переменных, например:. Стандартным видом одночлена назовем такое представление этого одночлена, когда на первом месте стоит числовой множитель, а далее идут степени переменных. Пример 1 Найти стандартный вид одночлена. Используя определение степени и коммутативность умножения находим:. Приведем пример многочлена:.






